¿Para qué sirve una derivada?
Creo que no soy la única que durante mis años escolares memorizó sin ton ni son un montón de conceptos y procedimientos sin saber si quiera qué eran.
Yo, que era bastante buena en matemáticas, llegué a Bachillerato y suspendí el trimestre en el que me "explicaron" las derivadas y las integrales, básicamente porque no entendía qué eran o cuál era su utilidad.
Hoy, y a pesar de no haber necesitado una derivada en vida, entiendo que son esenciales para muchas profesiones, así que, si nunca supiste qué son en realidad, a ver si hay suerte si te lo explica alguien de letras...
Derivadas para gente de letras
Qué hay que saber: Una función es la relación numérica entre dos variables si una depende de la otra.
Por ejemplo: Si compro una silla me gasto 10 euros, si compro dos son 20, si compro 33 son 330...
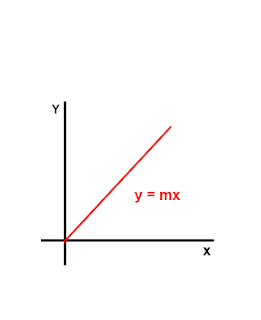
La representación gráfica sería la siguiente:
Pero no todas las relaciones son tan fáciles (¿a que no?)
Hay funciones de esas que suben y bajan, se curvan y se ponen negativas... Por ejemplo, nos vamos de senderismo, por una ruta de 15 km, sabiendo que la velocidad media de un ser humano es de 5km/h, creemos que vamos a tardar 3 horas. Pero, hemos ido más lentas en las subidas, nos hemos parado a echarnos un selfie en el mirador y hemos echado una carrera en el llano por lo que al final, hemos tardado 4 horas. Imaginad que alguien hace una representación gráfica de lo ha sido nuestra excursión:
En este caso, estamos relacionando velocidad (y) con el tiempo (x).
Por lo que sea, queremos saber cuál ha sido la aceleración en un momento determinado, o la variación en nuestra velocidad en un intervalo de tiempo, bien, pues para "averiguarlo" debemos aplicar la famosa derivada que no es más que una derivada de la función original (aquí no se comieron mucho el tarro para ponerle nombre) Es decir, si estamos relacionando velocidad con tiempo al derivar obtendríamos la aceleración. Es como otra vuelta de tuerca.
Ésto que puede parecer tan abstracto es sumamente útil para calcular la velocidad de los cambios en procesos físicos, cómo se modifica la economía o las variaciones que va realizando un ciclista durante la carrera.
Por ejemplo: Si compro una silla me gasto 10 euros, si compro dos son 20, si compro 33 son 330...
La representación gráfica sería la siguiente:
Pero no todas las relaciones son tan fáciles (¿a que no?)
Hay funciones de esas que suben y bajan, se curvan y se ponen negativas... Por ejemplo, nos vamos de senderismo, por una ruta de 15 km, sabiendo que la velocidad media de un ser humano es de 5km/h, creemos que vamos a tardar 3 horas. Pero, hemos ido más lentas en las subidas, nos hemos parado a echarnos un selfie en el mirador y hemos echado una carrera en el llano por lo que al final, hemos tardado 4 horas. Imaginad que alguien hace una representación gráfica de lo ha sido nuestra excursión:
En este caso, estamos relacionando velocidad (y) con el tiempo (x).
Por lo que sea, queremos saber cuál ha sido la aceleración en un momento determinado, o la variación en nuestra velocidad en un intervalo de tiempo, bien, pues para "averiguarlo" debemos aplicar la famosa derivada que no es más que una derivada de la función original (aquí no se comieron mucho el tarro para ponerle nombre) Es decir, si estamos relacionando velocidad con tiempo al derivar obtendríamos la aceleración. Es como otra vuelta de tuerca.
Ésto que puede parecer tan abstracto es sumamente útil para calcular la velocidad de los cambios en procesos físicos, cómo se modifica la economía o las variaciones que va realizando un ciclista durante la carrera.



Comentarios
Publicar un comentario